
안녕하세요
27년차 진로탐색꾼 조녁입니다!
오늘은 텐서플로우 자격증 과정 네번째 강좌인
'Sequences, Time Series and Prediction '
1주차 강의(Sequences and Prediction) 및 자료를 공부했습니다.
어느덧 코스4에 왔네요!! 시계열만 공부하면 이제 드디어 끝입니다!!!
이번에는 시퀀스 모델 중에 시계열 , 즉 시간이 지남에 따라 변화할 값들을 예측해볼 것입니다. eg) 주식시장의 흐름, 날씨 등
마지막에는 sunspot activity에 대해서 직접 다뤄볼 것입니다.(주기가 11년이든 22년이든!)
첫번째 영상, Time series examples
시계열 데이터는 주식 가격 변동, 날씨의 변화 , 무어의 법칙과 같은 역사적 동향에서 살펴볼 수 있다.
또한 일본인 사망-출생 그래프와 이산화탄소배출과 지구 온도 그래프와 같은 그래프를 살펴보자.
이러한 다변량 그래프는 서로의 상관관계를 포함하여 보여줄 수 있다.

또한 아래의 자동차의 이동을 살펴보자. 이때 자동차의 이동은 위도(Latitude)(y좌표)와 경도(Longitude)(x좌표)의 변화로 나타낼 수 있다.
그러나 가속도를 표현하기 위해선 일변량 그래프가 아닌 다변량 계산이 필요하다. (여기선 기울기 = y증가량/x증가량)

두번째 영상, Machine learning applied to time series
우리는 이 시계열 분석을 통해 미래를 예측하거나(그림3. 일본의 고령화 예측) , imputation(그림4Imputation) 할 수 있다.
또한 시계열 예측을 사용하여 로그에 찍히는 이상을 감지할 수 있다.(그림5. 로그 이상 탐지)
*Imputation : 빈부분을 대체하여 메꾸는 행동



세번째 영상, Common patterns in time series
trend(추세) , seasonality(주기) , Autocorrelation , Noise 와 같은 현상들이 있을 수 있다.
노이즈를 제외하면, 시계열에서도 패턴을 찾으면 그것으로 예측할 수 있다.(다만 과거에 있는 일이 미래에도 일어날 거란 가정하에)

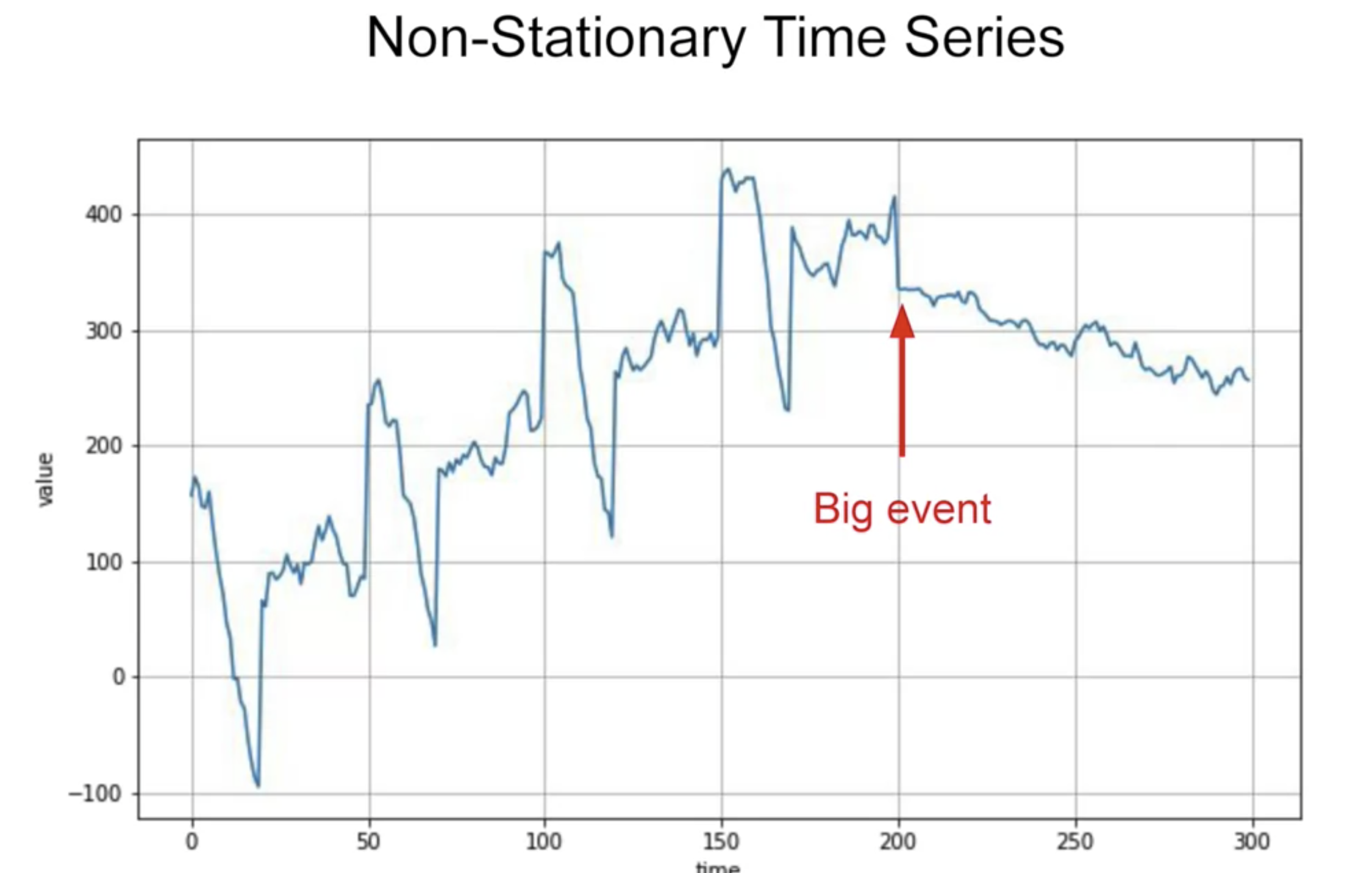
그러나 실제 시계열에선 아래와 같은 경우(Non-Stationary Time Series, 비고정식 시계열)도 일어난다. 분명 특정 시점까지는 트렌드도 있고 주기도 있었지만, 특정 시점이후로는 하락하고 있다. 이것을 주식시장이라고 본다면, 아마 코로나 펜데믹, 금융위기와 같은 사건 이후 상황이 달라지는 현상으로 미루어 볼 수 있다.
이런 경우, Big event 이후 기간(200~300 time)을 고정시켜 학습하는 것이 더 좋은 결과를 도출할 것이다.
머신러닝에서 데이터가 많을수록 좋다고 배웠지만(실제로 고정식 시계열에선 그렇다.) 아래와 같은 비고정식에서는
학습의 기준을 어디로 잡느냐가 중요하다.
이제 위와 같은 합성된 시계열 그래프를 통합문서로 살펴볼 것이다. 그리고 실제 데이터를 다루기 전에, 몇 가지 예제를 다뤄볼 것이다.
네번째 영상, Introduction to time
여러가지 상황을 합성시켜서 그래프의 변화를 살펴봤다.
우리는 이러한 합성이 머신러닝을 통해 시계열 데이터를 예측함에있어서 필수적인것을 배웠다. (실제 데이터는 복합적이기때문에)
다섯번째 읽기자료, Introduction to time series notebook
gist.github.com/jonhyuk0922/57d0eae8a8ab379b85be5462cf7695d4
S+P_Week_1_Lesson_2.ipynb의 사본
S+P_Week_1_Lesson_2.ipynb의 사본. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
여섯번째 영상, Train, validation and test sets
fixed partitioning : 예측 모델의 성능을 확인하기 위해 시계열을 train, validation ,test period로 나눈다.

roll-forward partitioning : 조금씩 훈련 범위를 늘려간다. 학습한 모델로 유효검증 범위를 예측한다.

그림9와 같이 조금씩 training period를 늘려가면서 재학습을 진행한다. 예를 들어, 트레이닝 피리어드를 기반으로 벨리데이션 피리어드로 성능을 확인한다. 그리고 나서 벨리데이션 피리어드를 포함하여 다시 학습시킨다. 학습한후, 테스트 피리어드로 성능을 검사한다. 그리고 다시 테스트 피리어드를 학습시킨다. 이러한 과정을 반복하다보면 아래 그림10과 같이 범위가 변경된다.
이렇게 하는 이유는, 그림8 이나 그림9처럼 처음에 잡은 범위대로 하고 test period를 학습시키지 않으면 손해기 떄문이다. (우리가 예측하고 싶은 부분에 가장 가까운 부분이 test Period 였으므로)

일곱번째 영상, Metrics for evaluating performance

여덟번째 영상, Moving average and differencing
Moving Average : 설정한 Averaging Window (예를 들어 30days) 안에서 평균값을 취한다. (그림12 참조)
많은 노이즈를 없애주지만, 추세와 계절성은 없애지 않는다. 하지만 미래 예측에 있어서는 naive forecast보다 더 나쁠 수 있다.

mae : 7.14
위 그림12에서 에러를 줄이기 위한 방법 중 하나는 differencing 이다.
differencing : 시간의 단위가 1년이든, 한달이든, 하루든, 현재 t에서 365를 뺀 값과의 차이를 plot한다. 이렇게 하면 추세와 계절성이 없어진다.

그 다음, 그림13위에 moving average를 취해준다. 그러면 아래 그림14와 같은 그래프가 나온다. 그러나 이 값들은 그림12에서 사용한 원래 값들이 아니다. 이제 원래 값들을 대상으로 적용해보겠다.

그림12 그래프에 differencing을 취해서 moving average를 취해주면 아래 그림15와 같다. 괜찮지 않은가?
mae는 5.8로 그냥 moving average를 취해줬을 떄의 값 7.14 보다 감소한 것을 확인할 수 있다.

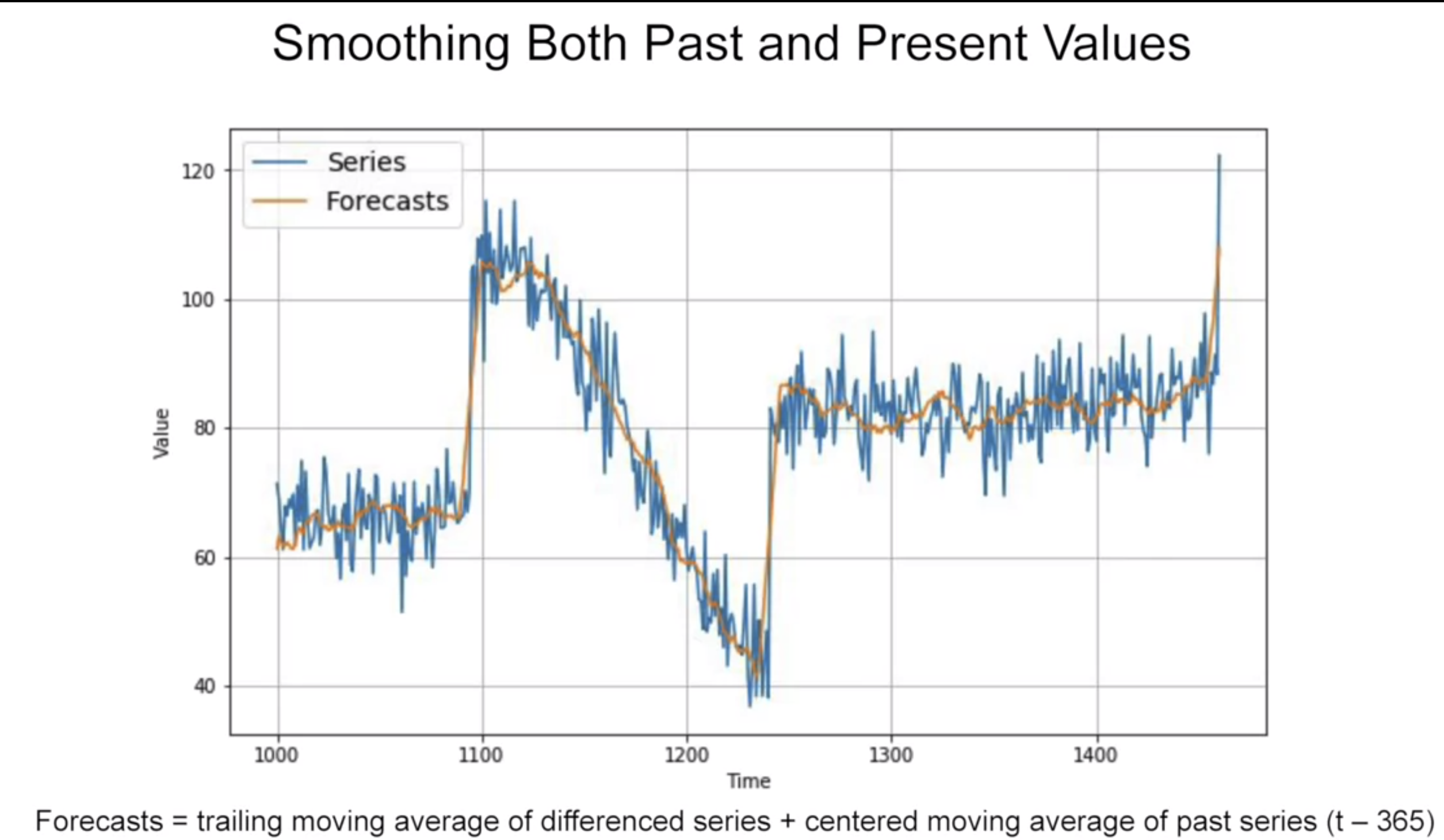
하지만 아직 노이즈가 남아있는 것을 볼 수 있다.그래서 과거 값으로부터의 노이즈를 제거하기 위해 과거(t-365)값들의 중앙값으로 더해준다.
아래 그림16과 같이 매끄러운 예측 그래프를 확인할 수 있다.
아홉번째 영상, Trailing versus centered windows
t-32, t-1에서 현재 값의 이동 평균을 계산할 때 후행 창(trailing window)을 사용할 때 유의하십시오.
그러나 중앙 창(centered window)을 사용하여 1 년 전의 과거 값의 이동 평균을 계산하면 t-1 년-5 일, t-1 년 + 5 일이됩니다.
그러면 중앙 창을 사용하는 이동 평균이 후행 창을 사용하는 것보다 더 정확할 수 있습니다. 그러나 미래 가치를 모르기 때문에 현재 가치를 매끄럽게하기 위해 중앙 창을 사용할 수 없습니다. 그러나 과거 값을 매끄럽게하기 위해 중앙 창을 사용할 수 있습니다.
열번째 영상, Forecasting
아래 주어진 노트북에 대한 코드 리뷰
열한번째 읽기자료, Forecasting notebook
S+P Week 1 - Lesson 3 - Notebook.ipynb의 사본
S+P Week 1 - Lesson 3 - Notebook.ipynb의 사본. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
퀴즈에서 배운점

* auto correlation 이란?
en.wikipedia.org/wiki/Autocorrelation
Autocorrelation - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search correlation of a signal with a time-shifted copy of itself, as a function of shift Above: A plot of a series of 100 random numbers concealing a sine function. Below: The sine function
en.wikipedia.org
1주차 마무리
This week you explored the nature of time series data, and you saw some of the more common attributes of them, including things like seasonality and trend. You looked at some statistical methods for predicting time series data also.
Next week you're going to start to look into using DNNs for time series classification, including the important tasks of understanding how to break up a time series into training and validation data!
과제 :시계열 데이터 예측하기
window_size를 10이 아닌 6으로 해주니 더 작은 오류가 발생함.
Course4-Week 1- Exercise- Answer
Course4-Week 1- Exercise- Answer. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
'머신러닝 & 딥러닝 공부 > Tensorflow' 카테고리의 다른 글
| [Tensorflow dev 자격증] Recurrent Neural Networks for Time Series (0) | 2021.03.02 |
|---|---|
| [Tensorflow dev 자격증] Deep Neural Networks for Time Series (0) | 2021.03.02 |
| [Tensorflow dev 자격증] Sequence models and literature (0) | 2021.02.25 |
| [Tensorflow dev 자격증] Sequence models (0) | 2021.02.24 |
| [Tensorflow dev 자격증] Word Embeddings (1) | 2021.02.17 |



